Conceptos Básicos
La Geometría Analítica fue iniciada y desarrollada por el matemático y filósofo René Descartes. Por eso a este sistema de ejes coordenados también se le conoce como "Sistema Cartesiano".
Sistema de ejes coordenados rectangulares. Dos rectas que se cortan se encuentran en un mismo plano. Si las líneas son perpendiculares entre sí tenemos lo que se llama un sistema de ejes coordenados rectangulares.
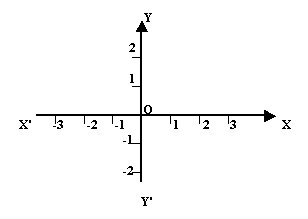
Par Ordenado
Es un conjunto de dos elementos a los cuales se les considera el orden en el cual aparecen. A los elementos se les denomina componentes.
( x ; y )
donde: x = 1er componente
y = 2do componente
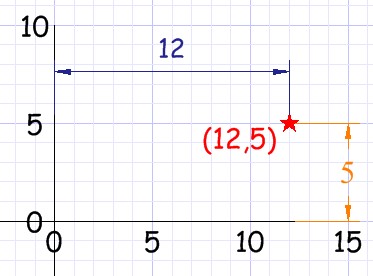
Sistema Coordenado Cartesiano
Un punto en el plano cartesiano se determina mediante el par P(x;y)
El sistema de coordenadas en el plano consiste en un par de rectas orientdas perpendiculares, llamadas ejes coordenadas.
Recta Horizontal: Eje de Abscisas ó Eje de X
Recta Vertical: Eje de Ordenadas ó Eje de Y
El punto de intersección de las abscisas y ordenadas se llama Origen (0;0)
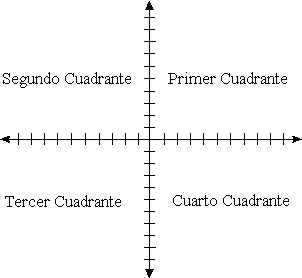
Las cuatro partes en que el plano queda dividido por los ejes coordenados se llaman cuadrantes (I, II, III, IV)
Para representar los puntos en el plano, necesitamos dos rectas perpendiculares, llamados ejes cartesianos o ejes de coordenadas:

El eje horizontal se llama eje X o eje de abscisas.
la denomina coordenada x del punto o abscisa del punto.
La segunda coordenada se mide sobre el eje de ordenadas, y se
le llama coordenada y del punto u ordenada del punto.

El eje horizontal se llama eje X o eje de abscisas.
El eje vertical se llama eje Y o eje de ordenadas.
El punto O, donde se cortan los dos ejes, es el origen de coordenadas.
Las coordenadas de un punto cualquiera P se representan por (x, y).
La primera coordenada se mide sobre el eje de abscisas, y sela denomina coordenada x del punto o abscisa del punto.
La segunda coordenada se mide sobre el eje de ordenadas, y se
le llama coordenada y del punto u ordenada del punto.
Los ejes de coordenadas dividen al plano en cuatro partes iguales y a
cada una de ellas se les llama cuadrante.
cada una de ellas se les llama cuadrante.

Signos
| Abscisa | Ordenada | |
|---|---|---|
| 1er cuadrante | + | + |
| 2º cuadrante | − | + |
| 3er cuadrante | − | − |
| 4º cuadrante | + | − |

El origen de coordenadas, O, tiene de coordenadas: O(0, 0).

Los puntos que están en el eje de ordenadas tienen su abscisa igual a 0.

Los puntos situados en el eje de abscisas tienen su ordenada igual a 0.

Los puntos situados en la misma línea horizontal (paralela al eje de abscisas) tienen la misma ordenada.

Los puntos situados en una misma línea vertical (paralela al eje de ordenadas) tienen la misma abscisa.
EjercicioRepresenta en los ejes de coordenadas los puntos:
A(1, 4), B(-3, 2), C(0, 5), D(-4, -4), E(-5, 0), F(4, -3), G(4, 0), H(0, -2)

Ubicación de puntos en el plano cartesiano
Realiza los siguientes ejercicios
I. Gráfica y di en qué cuadrantes se localizan los siguientes puntos:
1. S (-4.5,-2.5) 2. U (9/4,-4/2) 3. W (13/16,-7/3)
4. O (-8,10) 5. N (4,0) 6. A (5,-1) 7. A (0,8)
Representa gráficamente los siguientes triángulos, formados por las coordenadas de sus vértices.
a) A (4, 5), B(-7, 0), C(-6, 4) b) A(-3, 6), B(6, 5), C(-4,-3)
V. Grafica los siguientes polígonos cuyos vértices son:
a) A(-4, 2), B(-1,-3), C(2, -6), D(0, 4) b) A(-3, -5), B(5, -2), C(5, 5), D(1, 5) E(-4, 2)
Encuentra la figura formada por los siguientes puntos
Sistema de coordenadas polares
Un sistema de coordenadas polares es un sistema de coordenadas de dos dimensiones, en donde cada punto en ese plano está determinado por un ángulo llamado ángulo polar, formado desde un eje (llamado eje polar, equivalente al eje x del sistema coordenado) y una distancia de un punto al origen llamado polo
Esto indica que los puntos representados en este sistema polar corresponden a un par de coordenadas (r, θ)
Ejemplo
Representa en un sistema de coordenadas polares en el plano, el centro de referencia (punto O) y la línea OL sobre la que se miden los ángulos y los puntos (3,60º) y (4,210º).
El punto (3, 60º) indica que está a una distancia de 3 unidades desde O, medidas con un ángulo de 60º sobre OL.
El punto (4, 210º) indica que está a una distancia de 4 unidades desde O y un ángulo de 210º sobre OL.
Fuentes:
Módulo de aprendizaje Matemáticas 3 colegio de Bachilleres
del Edo de Sonora
Antología de Geometría Analítica de la Dgeta
Matemáticas 3, Eduardo Basurto Hidalgo Ed.
Pearson
Matemáticas 3, Rene Jiménez Colegio de Bachilleres



No hay comentarios:
Publicar un comentario